프론트엔드 업무를 진행하다보면, 무수한 좌표들 가운데 최종 폴리곤 라인을 따야하는 경우가 왕왕 발생한다.
이때 사용하는 방법이 convex hull 알고리즘이다.
Convex Hull은 점 집합을 둘러싸는 최소한의 볼록 다각형을 찾는 컴퓨터 과학 알고리즘이다.
이 볼록 다각형은 주어진 점 집합을 포함하며 모든 내부 각이 180도 이하인 다각형이다.
Convex Hull은 다양한 응용 분야에서 사용되며, 기하학, 이미지 처리, 컴퓨터 비전, 로봇 공학, 지리 정보 시스템 (GIS) 등에서 사용된다.
Convex Hull을 찾는 알고리즘은 여러 가지가 있으며, 다음은 가장 널리 사용되는 두 가지 알고리즘이다.
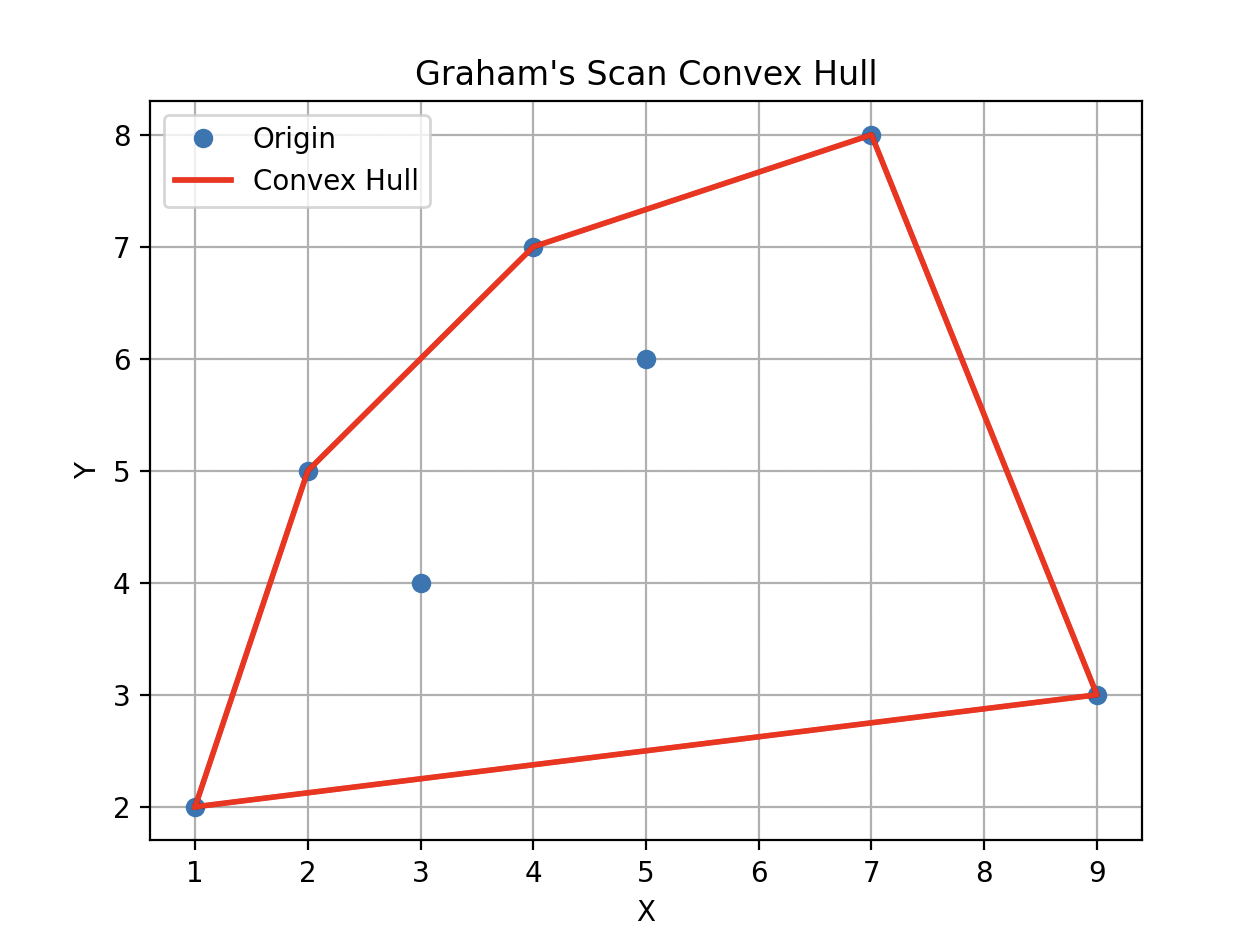
- Graham's Scan 알고리즘:
- 입력: 좌표 집합 배열
- 출력: Convex Hull을 형성하는 좌표의 목록 또는 순서
- 알고리즘:
- 좌표들 중에서 가장 아래에 있는 좌표를 찾아 시작점으로 선택.
- 모든 좌표들을 시작점을 기준으로 각도에 따라 정렬
- 정렬된 좌표들을 순회하면서 스택을 사용하여 Convex Hull을 구축.
- 스택에서 중간에 있는 좌표들을 제거하여 Convex Hull을 만든다.
- 파이썬 예제
더보기
import matplotlib.pyplot as plt
import numpy as np
def graham_scan(points):
def cross_product(o, a, b):
return (a[0] - o[0]) * (b[1] - o[1]) - (a[1] - o[1]) * (b[0] - o[0])
def sort_by_angle(p):
return np.arctan2(p[1] - pivot[1], p[0] - pivot[0])
if len(points) < 3:
return points
# 시작점 찾기 (가장 아래에 있는 점을 선택)
pivot = min(points, key=lambda point: (point[1], point[0]))
# 각도로 점들 정렬
sorted_points = sorted(points, key=sort_by_angle)
hull = [pivot, sorted_points[0]]
for point in sorted_points[1:]:
while len(hull) > 1 and cross_product(hull[-2], hull[-1], point) <= 0:
hull.pop()
hull.append(point)
return hull
# 좌표 배열 생성
points = np.array([(1, 2), (3, 4), (5, 6), (7, 8), (2, 5), (9, 3), (4, 7)])
# Convex Hull 계산
hull = graham_scan(points)
# 결과 출력
print("Convex Hull 점들:", hull)
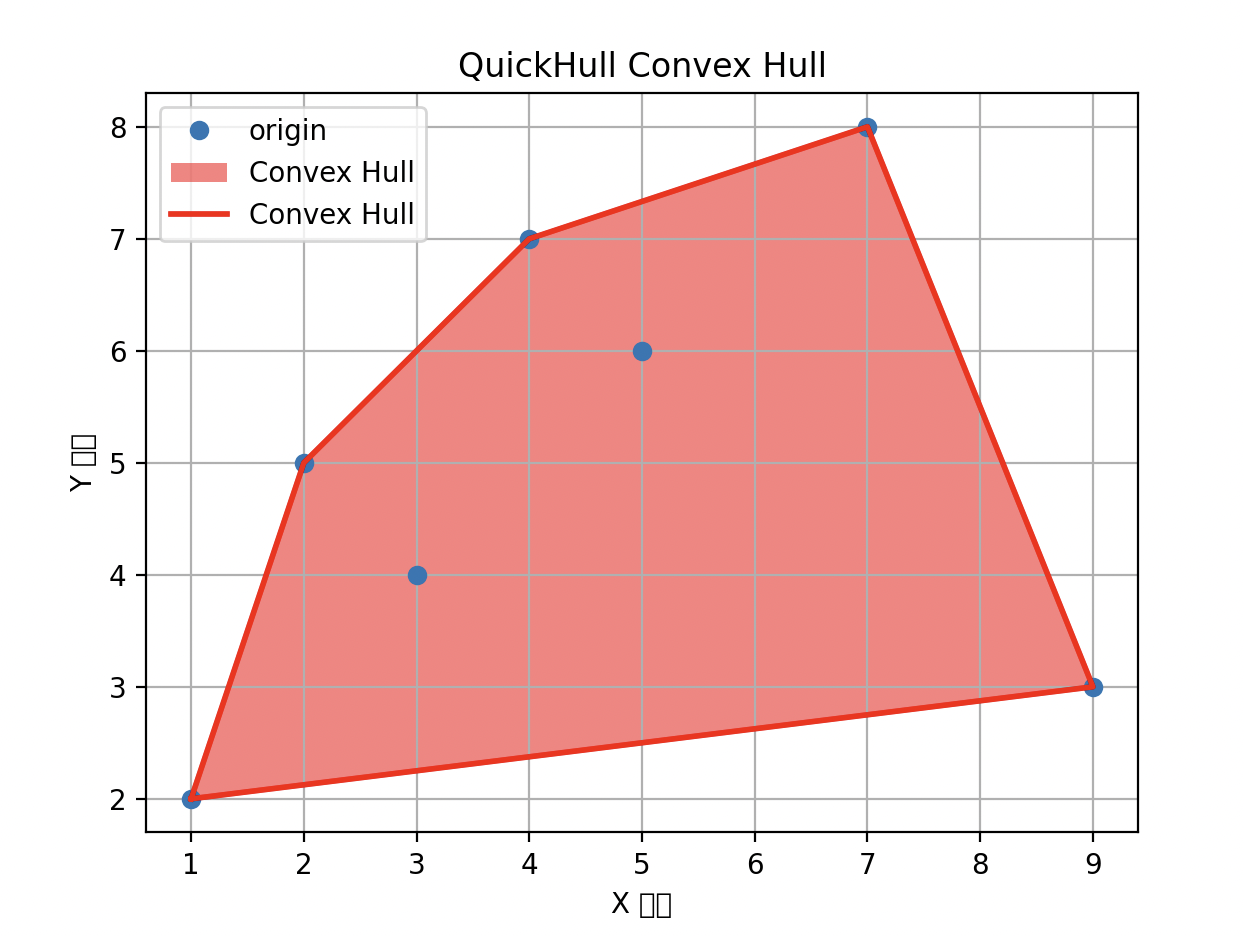
- QuickHull 알고리즘:
- 입력: 좌표 집합 배열
- 출력: Convex Hull을 형성하는 좌표의 목록 또는 순서
- 알고리즘:
- 점들 중에서 가장 왼쪽과 오른쪽에 있는 점을 찾아서 시작점과 끝점으로 선택합니다.
- 시작점과 끝점을 연결하는 직선을 기준으로 점들을 두 개의 부분집합으로 나눕니다.
- 각 부분집합에 대해 재귀적으로 Convex Hull을 찾고 합칩니다.
- Convex Hull을 합칠 때, 양 끝의 점을 찾아 연결하여 Convex Hull을 완성합니다.
- 파이썬 예제
더보기
import numpy as np
from matplotlib import pyplot as plt
def quick_hull(points):
def find_hull(points, p1, p2):
if not points:
return []
# p1과 p2로 형성된 선에서 가장 먼 점을 찾습니다.
farthest_point = max(points, key=lambda point: distance(p1, p2, point))
# 점들을 두 부분집합으로 나눕니다.
subset1 = [point for point in points if is_left(p1, farthest_point, point)]
subset2 = [point for point in points if is_left(farthest_point, p2, point)]
# 두 부분집합에 대해 볼록 껍질을 재귀적으로 찾습니다.
hull1 = find_hull(subset1, p1, farthest_point)
hull2 = find_hull(subset2, farthest_point, p2)
# 두 볼록 껍질을 결합합니다.
return hull1 + [farthest_point] + hull2
def distance(p1, p2, p3):
x1, y1 = p1
x2, y2 = p2
x3, y3 = p3
return (x2 - x1) * (y3 - y1) - (x3 - x1) * (y2 - y1)
def is_left(p1, p2, p3):
return distance(p1, p2, p3) > 0
if len(points) < 3:
return points
# 두 개의 극단점을 찾습니다 (가장 왼쪽과 가장 오른쪽).
leftmost = min(points, key=lambda point: point[0])
rightmost = max(points, key=lambda point: point[0])
# 점들을 두 부분집합으로 나눕니다.
left_subset = [point for point in points if is_left(leftmost, rightmost, point)]
right_subset = [point for point in points if is_left(rightmost, leftmost, point)]
# 각 부분집합에 대한 볼록 껍질을 찾습니다.
left_hull = find_hull(left_subset, leftmost, rightmost)
right_hull = find_hull(right_subset, rightmost, leftmost)
# 두 볼록 껍질을 결합합니다.
return [leftmost] + left_hull + [rightmost] + right_hull
# 예제 사용법
points = np.array([(1, 2), (3, 4), (5, 6), (7, 8), (2, 5), (9, 3), (4, 7)])
hull = quick_hull(points)
# 결과 출력
print("Convex Hull 점들:", hull)
위 예제 코드 및 알고리즘이야 인터넷을 통해 검색해서 충분히 알 수 있지만, 퍼포먼스 측면에서는 매우 손해다.
실제 사용할때에는 파이썬이나 노드Js의 경우 라이브러리를 사용하여 간결하고 쉽게 사용할 수 있다.
아래는 파이썬 예제 코드이다.
from scipy.spatial import ConvexHull
# 좌표 배열 생성 (예: [(x1, y1), (x2, y2), ...])
a = [(1, 2), (3, 4), (5, 6), (7, 8), (2, 5), (9, 3), (4, 7)]
# Convex Hull 계산
hull = ConvexHull(a)
# Convex Hull의 꼭짓점 좌표 출력
print("Convex Hull의 꼭짓점 좌표:")
for vertex in hull.vertices:
print(a[vertex])
-------------------------------------
결과)
Convex Hull 좌표:
(1, 2)
(9, 3)
(7, 8)
(4, 7)
(2, 5)중요한건 최외곽을 따는 알고리즘이 convex hull 알고리즘이라는 것을 알면 추후에 검색을 통해 쉽게 사용할 수 있으니,
이 부분만 잘 기억하자!
반응형
'학습' 카테고리의 다른 글
| 이미지 기하학적 변환 (1) | 2024.02.16 |
|---|---|
| [Python] 프레임 이미지 이용 동영상 비디오 만들기 (0) | 2024.02.08 |
| 키즈노트 일괄 다운로드 방법 ( 사진, 알림노트 ) (1) | 2024.01.28 |
